AP® Computer Science A Lecture 4
Presented by TU RUIXUAN
Copyright © TU RUIXUAN, All Rights Reserved
Tailored for College Board® Advanced Placement® Program
According to Course and Exam Description Effective Fall 2020
Contents (AP CED Equivalent)
- Practice
H 4.1: Time
- Description
- There are n persons waiting in queue for lunch, and ti (i∈[1,n]) is the estimated waiting time for person numbered i.
- Please calculate the minimal total time cost by all persons in queue.
- Input Format
- Line 1 contains an integer n.
- Line 2 contains n integers of ti.
- Output Format
- Line 1 contains the minimal total waiting time.
- Useful Function
// java.util.Arrays public static void sort(int[] arr, int from_Index, int to_Index)
↓ Sample ↓
Sample Input
10
56 12 1 99 1000 234 33 55 99 812
Sample Output
2919
H 4.2: Family
- Description
- A family contains at least two persons (sometimes a.k.a. parents) or more if they have a child or children.
- In a family tree, we pretend all assets of a couple belongs to one of them and ignore another, but we treat the last generation of children who have not married seperately.
- There are n persons in the family tree, and every person has a name ai, assets which value bi, and a list of descendants li with a length of ei.
- In general, parents, grandparents, and ancestors can borrow money from their descendants.
- You will have m queries of persons, and you should give the amount of assets si that each person qi can use in maximum respectively.
↓ Format ↓
- Input Format
- Line 1 contains an integer n.
- Line 3i+2 (i∈[0,n)) contains a string pi, the parent's name. (For the first person, ROOT, as no one is on the tree)
- Line 3i+3 contains a string ai, the person's name.
- Line 3i+4 contains two integers bi, the value of assets.
- Line 3n+2 contains an integer m, the number of queries.
- Line 3n+3 to 3n+2+m contains m integers of qi, the asked names.
- Output Format
- There are m lines of output, and every line contains an integer si.
↓ Sample ↓
Sample Input (SCROLL)
6
ROOT
Mark
3
Mark
Mike
5
Mark
Kevin
8
Kevin
Smith
2
Kevin
Cindy
9
Cindy
Alex
3
3
Mark
Kevin
Cindy
Sample Output
30
22
12
↓ Explaination ↓
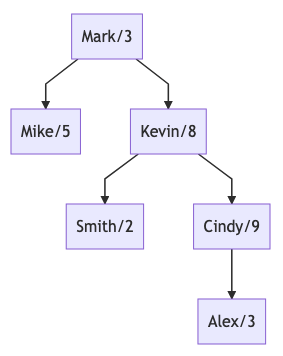
- Query 1: Mark/A=Mark+Mike+Kevin/A=3+5+8+2+9+3=30
- Query 2: Kevin/A=Kevin+Smith+Cindy/A=8+2+9+3=22
- Query 3: Cindy/A=Cindy+Alex=9+3=12
↓ Note ↓
- Except for the first person, there will be no parent name that appears before declaration.
- There will be at least one person on the tree.
- Please contain all classes into one source file. However, there can be only one
public class, so other auxiliary classes without themainfunction should be declared asclass.
H 5.1: Cubic
(© China National Olympiad in Informatics in Provinces)
- Description
- The format of a cubic equation is ax3+bx2+cx+d.
- You are given a, b, c, and d, and the equation has three solutions. The absolute value of the difference of any two solutions is larger than 1. All solutions are in [−100,100].
- Please note, for two points x1 and x2 (x1<x2) of a cubic function f(x)=0, if f(x1)⋅f(x2)<0, there should be a solution between x1 and x2.
- Please calculate the three real solutions of the equation.
- Input Format
- A line contains four real numbers a, b, c, and d.
- Output Format
- A line contains three real solutions from the minimum to the maximum. (all formatted with two digits after decimal point)
↓ Sample ↓
Sample Input
1 -5 -4 20
Sample Output
-2.00 2.00 5.00
H 5.2: FamilyR
Description
Most of the intended desciption is the same as H 4.2, so here is a list of differences:
- Any couple is treated as two persons, and they share their assets;
- Any person can have zero, one, or two parent(s) on the tree;
- Ancestors can only use assets from their descendants who has gender 1 and who has gender 0 and have not married;
- There will be names that appear before declaration;
- Only add the assets of one person once;
- A couple do not have to have different genders, but there can be only one partner at maximum for anyone;
- Parents of a person is a couple by default;
- Any person has no asset by default;
- Parent(s) and partner of a person can be set for more than one time;
- Any married person does not have any descendant who has one parent;
- Even if a couple changes, their relations to descendants do not change.
↓ Format ↓
- Input Format
- Line 1 contains an integer n, the number of operations.
- Line 1+i contains a string si, the operation command.
- The format of the operation command string follows:
1 p g: the person named p who has a gender g has no parent on the tree;2 a p g: the person named a is the only parent of the person named p who has a gender g;3 a b p g: the two persons named a and b are parents of the person named p who has a gender g;4 a b: the two persons named a and b are a couple;5 p x: the person named p has assets valued x;6 a: print all available assets of the person named a.
- Ranges: n∈[1,28], i∈[1,n], g∈[0,1]
- Output Format
- There are m lines of output, and every line contains an integer which is all available assets of the required person.
- Range: m∈[0,n]
↓ Sample ↓
Sample Input (SCROLL)
27
4 Kevin Cindy
4 Mike Daisy
4 Robert Roberta
1 Mark 1
2 Mark Mike 1
3 Robert Roberta Dale 1
2 Dale Daisy 0
3 Mike Daisy Emma 0
2 Mark Kevin 1
1 Robert 1
1 Roberta 0
3 Robert Roberta Cindy 0
3 Kevin Cindy Fran 1
5 Mark 3
5 Robert 5
5 Roberta 3
5 Mike 5
5 Kevin 8
5 Cindy 7
5 Fran 4
5 Dale 9
5 Daisy 2
5 Emma 6
6 Dale
6 Daisy
6 Mike
6 Mark
Sample Output
11
13
13
35
↓ Explaination ↓
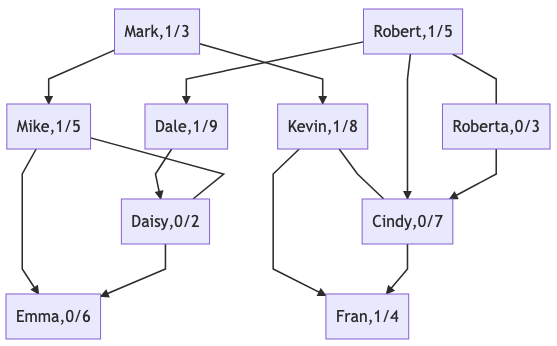
- Query 1: Dale/A=Dale+Daisy=11
- Query 2: Daisy/A=Daisy+Mike+Emma=13
- Query 3: Mike/A=Daisy/A=13
- Query 4: Mark/A=Mark+Mike/A+Kevin+Cindy+Fran=3+13+8+7+4=35
H 6.1: Schedule
- Description
- There are n courses on the schedule and m pairs as p of conditions
- For p=(a,b), course a cannot be taken simutaniously with course b
- For p=(−a,b), if course a is not taken, b cannot be taken
- Similar conditions applies to p=(a,−b) and p=(−a,−b)
- Please find if there is any conflict in the schedule
- If not, give a possible solution that satisfies all conditions
- Input (line number L)
- L=1: two integers n, number of variables, and m, number of conditions
- L=2→L=n+1: two integers a and b
- Output (line number L)
- L=1:
POSSIBLEorIMPOSSIBLE - L=2: n integers xi (xi∈[0,1]) for the condition (true or false) of the i-th course for a valid set of solution
- L=1:
↓ Sample ↓
Sample Input #1
2 3
1 2
2 -1
-1 -2
Sample Output #1
POSSIBLE
0 1
Sample Input #2
2 4
1 2
-1 2
1 -2
-1 -2
Sample Output #2
IMPOSSIBLE
H 6.2: Score
- Description
- Scores of the AP course should be curved. You are given a list of students, and please curve the score for every student.
- Grade levels include A (> 2 sd), B (≤ 2 sd, > 1 sd), C+ (≤ 1 sd, > 0), C- (≤ 0, > -1 sd), D (≤ -1 sd, > -2 sd), and F (≤ -2 sd) with equal width values on the normal distribution graph.
- Input (line number L)
- L=1: an integer n, number of operations
- L=2→L=n+1: operations (sequence is not guaranteed)
- Operations (
a:String,b:double)1 a b: Studentahas a raw scoreb2 a: Get the info of studenta(name, curved level, percentile, and raw score) (ifais not exist, do nothing)3: Get the info of the class (average raw score, average percentile, and standard deviation)
↓ Resources ↓
Resources
- Basic z-score Formula for One Sample: z=σx−μ (μ: mean, σ: standard deviation)
- Download for Package
org.apache.commons.math3: https://commons.apache.org/proper/commons-math/download_math.cgi - Sample Command
javac -cp "commons-math3.jar" Score.java- Unix:
java -cp "commons-math3.jar:." Score - Windows:
java -cp "commons-math3.jar;." Score
- Sample Code Snippet
import org.apache.commons.math3.distribution.*; double zScoreToPercentile(double zScore) { double percentile = 0; NormalDistribution dist = new NormalDistribution(); percentile = dist.cumulativeProbability(zScore) * 100; return percentile; }
↓ Sample ↓
Sample Input
13
1 A 96
1 B 98
1 C 95
1 D 94
1 E 99
1 F 93
3
2 A
2 B
2 C
2 D
2 E
2 F
Sample Output
95.83333333333333 49.209559169344416 2.3166067138525404
A C+ 52.867688560363426 96.0
B C+ 82.51769604168065 98.0
C C- 35.952769136435535 95.0
D C- 21.43589840606932 94.0
E B 91.41782334770656 99.0
F D 11.065479523810973 93.0
Thanks for Watching
Presented by TU RUIXUAN
Copyright © TU RUIXUAN, All Rights Reserved
AP® Computer Science A Series